Risk analysis: Le tecniche qualitative FMECA, HAZOP, FTA
| Appunti Chemicals | ||
| 12 Luglio 2025 | ||
| Salve Visitatore | ||
|
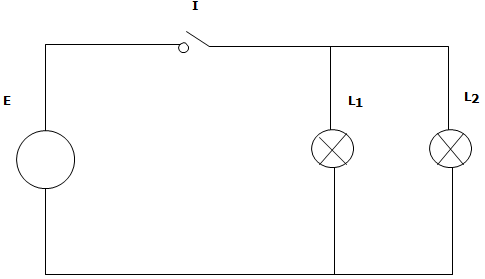
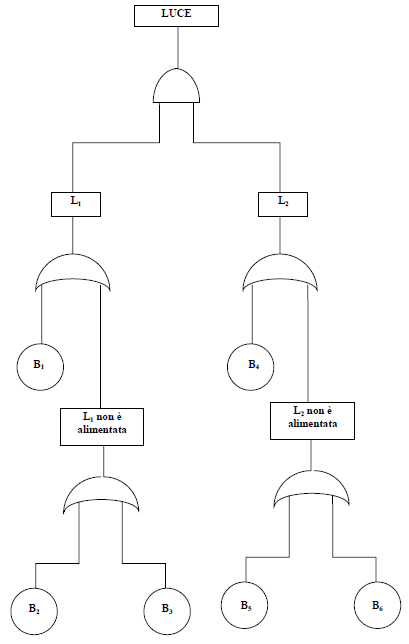
Risk analysis: Le tecniche qualitative FMECA, HAZOP, FTA Analisi di base delle tecniche qualitative di analisi dei rischi (Hazard Evaluation Procedures): Documenti Certifico FMEA | HAZOP |FTA - FMEA | IEC 60812 Premessa Le procedure quantitative hanno avuto un forte impulso soprattutto nella direzione della cosidetta analisi predittiva, ovvero aventi quale scopo la previsione su base probabilistica dei fenomeni. Le tecniche di tipo qualitativo, invece, sviluppatesi parallelamente alle precedenti, sono particolarmente adatte ad analizzare contesti applicativi. Mentre l’analisi quantitativa, infatti, richiede l’esame completo e sistematico di tutti i componenti in modo da identificare le fonti di rischio potenziale (hazards), l’analisi qualitativa risulta più flessibile nell’utilizzo. L’insieme delle tecniche qualitative viene detto, con terminologia anglo-sassone, Hazard Evaluation Procedures, e rappresenta - per l’appunto - l’insieme degli esami che possono essere condotti su di un sistema od impianto per studiare le combinazioni rischiose di materiali e/o processi in un assegnato ambiente operativo. Lo scopo della applicazione delle Hazard Evaluation Procedures consiste nell’identificare i possibili incidenti e stimare la loro frequenza. Per incidente si intende la sequenza di eventi imprevisti che conducono, mediante un meccanismo di concatenazione, al verificarsi di un evento non desiderato. Il primo evento della sequenza viene detto evento base e costituisce l’evento iniziale dal quale potrebbe scaturire una potenziale pericolosità. Grazie al fatto di considerare l’evento incidente come la conseguenza di una concatenazione di eventi, è possibile intervenire più agevolmente sul sistema nel senso di ridurre la possibilità del verificarsi di eventi imprevisti. Le conseguenze di un evento iniziale, infatti, possono essere ridotte ricorrendo ad analisi quantitative condotte sui singoli componenti del sistema (ad esempio, valvole, pompe, sensori, etc.). Quando un hazard è stato individuato, infatti, occorre valutarlo in termini di rischio nei confronti dei lavoratori, dell’ambiente e dell’azienda. A tale scopo occorre identificare l’evento base, gli eventi intermedi, di tipo propagativo o migliorativo, e le conseguenze di questi. Da questa analisi è possibile desumere anche gli interventi da effettuarsi per ridurre il rischio. La metodologia si basa sul lavoro di una squadra di esperti, dotati di differenti abilità tecniche e di varia estrazione scientifico-culturale. Il successo dell’applicazione dell’analisi Hazop, infatti, è strettamente legato ai seguenti fattori: - la completezza ed accuratezza dei dati utilizzati; I termini caratteristici dell’analisi hazop, inoltre, sono: - i nodi, cioè i parametri di processo fondamentali per l’individuazione del funzionamento del processo e dei suoi eventuali malfunzionamenti; Le parole guida comunemente impiegate sono le seguenti: - NO, ad indicare l’assenza totale dell’intenzione attesa; 3. FAULT TREE ANALYSIS (FTA) Lo studio prende avvio dall’individuazione dell’evento accidentale di guasto (si tratta del cosidetto top event il cui accadimento si vuole scongiurare) e, via via livello dopo livello secondo un approccio di tipo top-down, attraverso gli eventi intermedi fino ad arrivare a quelli di base. Ciò che differenzia tale analisi è la possibilità di intervenire con gli strumenti del calcolo al fine di individuare la soluzione dell’albero di guasto, consistente nella probabilità, o meglio la frequenza, di accadimento del top event a partire dai parametri probabilistici associati ai singoli eventi della catena considerata. Tale metodo, tra l’altro, è largamente utilizzato per l’analisi dei sistemi di sicurezza. Partendo dalla considerazione che ogni impianto o sistema è costituito da un certo numero di componenti elementari, si può supporre che tali componenti siano caratterizzati da un comportamento bistabile (o sono funzionanti o non sono funzionanti), così da poter attribuire a ciascuno di essi valore 1 o 0 a seconda dello stato funzionale. Gli elementi fondamentali per la costruzione dell’albero dei guasti sono, dunque, le porte logiche e gli eventi opportunamente rappresentati in base alla loro tipologia. Tutti questi contribuiscono a formare la catena degli eventi. In particolare, si avranno: - porte AND, che comportano il verificarsi dell’evento in output solamente quando si verificano tutti gli eventi in input; - porte OR, che rappresentano il verificarsi dell’evento in output quando si verifica almeno uno dei due eventi in input; - evento base, che è l’evento primario che non ha bisogno di ulteriori analisi ed approfondimenti; - evento primario, non sviluppato in una catena di eventi che potrebbero derivare da esso, perché non si hanno sufficienti informazioni e conoscenze; - evento intermedio, successivo all’evento base, esso può essere di tipo propagativo, se determina il verificarsi di successivi eventi dannosi, o migliorativo se determina, invece, un miglioramento generale dal punto di vista degli eventi accidentali; - top event, cioè l’evento di guasto le cui conseguenze, in termini di danni per gli uomini ed economici, sono gravi e da scongiurare. Il top event è normalmente un guasto, così come pure gli eventi intermedi e di base. I guasti possono essere così classificati: - guasti primari, che sono i guasti che si verificano in un contesto operativo normale e non possono essere quindi imputati a cause esterne (ad esempio, al rottura di un serbatoio operante in un range di pressioni normali, cioè nei limiti della pressione per il quale il serbatoio è progettato); - guasti secondari, che si verificano in un contesto operativo anomalo ed imputabili a particolari condizioni esterne (se, nel caso del serbatoio già visto, si manifesta una sovrapressione causata da un guasto esterno); - guasti di comando, che sono malfunzionamenti per i quali il componente opera propriamente ma in un tempo ed in uno spazio sbagliati. Gli eventi base sono generalmente guasti primari; i guasti secondari e di comando, invece, sono eventi intermedi che richiedono, cioè, un supplemento di indagine. L’applicazione della Fault Tree Analysis, in sostanza, consiste in una serie di passi, attraverso i quali si giunge alla costruzione dell’albero di guasto, alla definizione delle catene di eventi ed alla analisi quantitativa del top event. La prima azione da compiere consiste nell’individuazione del top event. Si tratta di un passo essenziale per il successo dell’analisi, dato che, in un’ottica di esame top down, è estremamente importante circoscrivere i casi da considerare. Come si usa dire, occorre valutare il What (che cosa), il Where (dove) ed il When (quando), cioè le tre W. Se si individuasse come top event un evento particolarmente generico, come un incendio od un esplosione, si correrebbe il rischio di effettuare un’analisi inefficace. La costruzione dell’albero di guasto, e quindi l’individuazione dei cammini di guasto, risulterebbe in tal caso lunga e poco utile ai fini della prevenzione o della protezione. Il passo successivo dell’analisi consiste nella costruzione dell’albero di guasto, basata sull’individuazione di tutti i possibili eventi intermedi fino ad arrivare agli eventi base, cioè alle cause prime di qualunque cammino. Tale operazione si effettua collegando logicamente gli eventi, cioè ricorrendo alle porte AND ed OR, dato che si è supposto che i componenti sono caratterizzati da comportamento bistabile. Per la rappresentazione grafica dell’albero si ricorre ad una simbologia pressoché universalmente riconosciuta. Costruito l’albero di guasto, ed una volta realizzata la sua rappresentazione grafica, è possibile passare alla soluzione dell’albero, consistente in una sua analisi finalizzata al calcolo della frequenza di accadimento del top event. Per la soluzione dell’albero si può procedere attraverso l’analisi dei minimal cut sets (cioè gli insiemi minimi di eventi base necessari e sufficienti a causare il top event), oppure mediante la metodologia gate by gate, d’altronde poco usata. Quest’ultima, infatti, è consigliata solamente quando si ha a che fare con strutture logiche particolarmente semplici, mentre alberi più grandi e complessi richiedono l’utilizzo del metodo dei minimal cut sets, spesso implementato sui calcolatori. L’analisi dei minimal cut sets è una tecnica attraverso la quale è possibile semplificare la struttura di un albero di guasto evidenziando così i cammini minimi che, a partire da un evento base, portano al top evento. In sostanza, si individuano tutte le possibili combinazioni di eventi base che conducono all’evento sfavorevole. La semplificazione avviene applicando le regole dell’algebra di Boole attraverso le quale si giunge a trovare un nuovo albero, più semplice da studiare, ma logicamente equivalente al precedente. Le proprietà dell’analisi logica di Boole, applicabili allo studio degli alberi di guasto nell’ottica di ricercare i minimal cut sets, sono le seguenti: proprietà commutativa A∪B = B∪A A∩B = B∩A proprietà associativa A∩(B∩C) = (A∩B)∩C A∪(B∪C) = (A∪B)∪C proprietà distributiva A∩(B∪C) = A∩B ∪ A∩C proprietà di assorbimento A∪A = A A∩A = A proprietà di idempotenza A∪A∩B = A Nelle precedenti relazioni A, B rappresentano due generici eventi e le notazioni di calcolo unione ∪ ed intersezione ∩ stanno ad indicare l’eventualità che A e B avvengano indipendentemente l’uno dall’altro o contemporaneamente, rispettivamente. Affinché sia possibile attuare questa metodologia, è necessario che siano verificate le seguenti condizioni: - i guasti considerati sono di natura binaria; Il modo più semplice ed immediato per capire il funzionamento della tecnica dei minimal cut sets è, sicuramente, quello di vedere una applicazione concreta del metodo. Si supponga di avere il circuito rappresentato nella Figura 2. Esso consiste di due lampade collegate in parallelo (L1 ed L2), un interruttore (I) ed un generatore (G). Il primo passo da compiere consiste nella costruzione dell’albero di guasto e, quindi, nell’individuazione del top event innanzi tutto. Supponiamo che l’evento di guasto da scongiurare sia l’assenza di luce, come è facile immaginare. Affinché si verifichi tale circostanza, le due lampade non devono funzionare, o perché le due lampade sono guaste o perché si verificano altri eventi, quali il guasto dell’interruttore o il guasto del generatore. L’albero di guasto rappresentativo del circuito della Fig. 2 e degli eventi appena descritti è presentato nella successiva Figura 3. Il passo successivo per trovare i minimal cut sets consiste nella determinazione delle equazioni analitiche rappresentative dell’albero. Tenuto conto del significato degli eventi base Bi: Fig. 2 - Esempio di applicazione per l’analisi dei Minimal Cut Sets
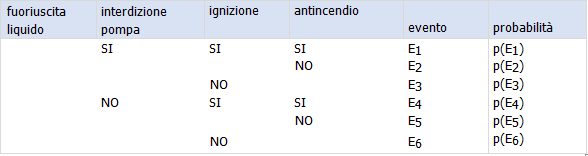
si giunge alla seguente equazione generale, in cui TE è il top event ed I1 e I2 sono gli eventi intermedi corrispondenti alle situazioni per cui le lampade L1 ed L2 non funzionano, rispettivamente: TE = I1 ⋅ I2 = [B1 + (B2 + B3)] ⋅ [B4 + (B5 + B6)] Poiché B2 = B5 e B3 = B6, si ha: TE = I1 ⋅ I2 = [B1 + (B2 + B3)] ⋅ [B4 + (B2 + B3)] e quindi, in base alle proprietà della logica di Boole: TE = B1 ⋅ B4 + B1 ⋅ (B2 + B3) + B4 ⋅ (B2 + B3) + (B2 + B3) ⋅ (B2 + B3) TE = B2 + B3 + (B1 + B4) (B2 + B3) + B1⋅ B4 e, infine: TE = B1⋅ B4 + (B2 + B3) dalla quale è possibile ricavare l’albero equivalente (Figura 4). L’equazione TE = B1⋅ B4 + (B2 + B3) rappresenta il numero minimo di cammini necessari e sufficienti a determinare il verificarsi del top event, come è facile provare. Fig. 4 - Albero equivalente dell’albero di Fig. 3 - entrambi le lampade L1 ed L2 sono guaste, oppure quando Al metodo dei minimal cut sets se ne aggiunge uno approssimato per analizzare l’albero dei guasti e valutare, con semplici calcoli, i dati statistici riguardanti il top event. Il criterio in questione, in realtà, è applicabile solamente quando le probabilità degli eventi base o dei minimal cut sets non sono troppo elevate (all’incirca maggiori di 0,1). In tal caso, infatti il criterio porterebbe a stime troppo prudenti, sovrastimando la probabilità di accadimento del top event. La procedura per analizzare un sistema, in definitiva, si esplica in una serie di passaggi di semplice comprensione, ove si sia già costruito l’albero dei guasti relativo: - definizione del sistema e dei suoi componenti; .... 4. ALBERO DEGLI EVENTI (EVENT TREE ANALYSIS) Un’altra metodologia di analisi molto comoda per schematizzare i sistemi e le situazioni che li possono riguardare è rappresentata dalla costruzione dell’albero degli eventi. Anche in questo caso, come per l’albero dei guasti, si ha a che fare con una struttura logica in grado di descrivere - in modo diagrammatico - tutti i potenziali cammini nei quali un evento può prodursi e svilupparsi in un sistema. La generica foglia dell’albero rappresenta un possibile scenario, che si verificherebbe in corrispondenza di una particolare combinazione di eventi che costituiscono il cammino considerato. Si tratta, in definitiva, di uno strumento ampiamente utilizzato in una metodologia di analisi più ampia, ed oggi divenuta particolarmente rilevante, detta analisi cause-conseguenze. In tale approccio, si definisce il top event e si costruisce l’albero dei guasti associati a questo specifico evento; si giunge, così, alla probabilità di accadimento del top event ed alle cause elementari che lo possono generare. Successivamente, si può costruire l’albero degli eventi che consente di evidenziare i possibili scenari evolutivi della circostanza considerata ed associare a ciascuno di essi le probabilità di accadimento. Un esempio può aiutare a capire il significato e la portata della event tree analysis. Si supponga di considerare un sistema per il trasferimento di combustibile liquido: esso è costituito da una pompa, una condotta ed un sistema antincendio. Il top event di questo sistema può assumersi la fuoriuscita del liquido dall’impianto. In tale caso, potrà limitarsi il danno, ad esempio, spegnendo la pompa. Ove non fosse possibile intervenire su tale dispositivo impiantistico, potranno verificarsi altri eventi contingenti, presi in esame dalla analisi. Innanzi tutto, esiste la possibilità che si inneschi l’incendio del combustibile fuoriuscito e, successivamente, occorrerà prendere in considerazione l’eventualità che il sistema antincendio entri in funzione. Diagramma delle situazioni appena prese in considerazione: Fig. 5 - Esempio di albero degli eventi Come è possibile constatare dal diagramma, vengono individuati gli eventi relativi al top event e ad essi viene associata una probabilità condizionata. Le probabilità, cioè, sono valutate sapendo che ad ogni nodo dell’albero, si verifica l’evento del nodo precedente. La generica probabilità p(Ei), dunque, è espressa come il prodotto delle probabilità degli eventi presenti sul ramo considerato. Ad esempio nel caso precedentemente visto, se consideriamo l’eventualità che si abbia fuoriuscita di combustibile e che questo non si incendi (evento E6), la probabilità relativa è la seguente: p(E6) = p(TE) ⋅ p(pompa off/TE) ⋅ p(no fire/pompa off e TE) L’esempio appena presentato costituisce una classica applicazione della event tree analysis. Oltre a calcolare la probabilità di accadimento dei possibili scenari, assai spesso è opportuno quantificare anche qualche altro aspetto che si vuole studiare come, ad esempio, eventuali danni economici che dovessero essere connessi.
|
||
 |
||
|
è un sito di INVIO NEWSLETTTER Se vuoi cancellarti dall'invio della newsletter oppure effettua il login al sito ed entra nella Tua Area Riservata, in “Modifica dati” agisci con la spunta sul box di selezione “Newsletter”. L'Elenco completo di tutte le ns newsletter è qui: Archivio newsletter |
||
  |
||
| Certifico Srl 2000-2018 | VAT IT02442650541 | ||